10 Iteration

Warning

This chapter was developed from scratch for the Fall 2022 semester. As such, you might notice a few extra typos, or some topics that are not well explained. If you encounter these issues, please let us know on the discussion forum. Except some additional changes to what is currently published while this warning persists.

In programming, iteration is the act of repeating a set of instructions. This can be done several different ways:

Repeat until some condition is met.
Repeat a specified number of times.
Repeat for each element of a collection.

In R, the last example here, repeating each element of a collection, is by far the most common because vectors (collections of elements) are the most important data structure in R. As such, R has built-in functions that make this type of iteration extremely easy. While R does provide the usual iteration abilities through the use of for and while loops, these should not be your go-to methods for performing iteration with R.

After reading this chapter you should be able to:

Use lapply and related functions to iterate over the elements of a vector.
Use for and while loops to repeatedly evaluate R expressions.
Avoid common pitfalls when using loops in R.

10.1 Apply Functions

One of the most common operations that you will encounter while programming with R is running a function with each element of some vector as input and then collecting the results in a vector.

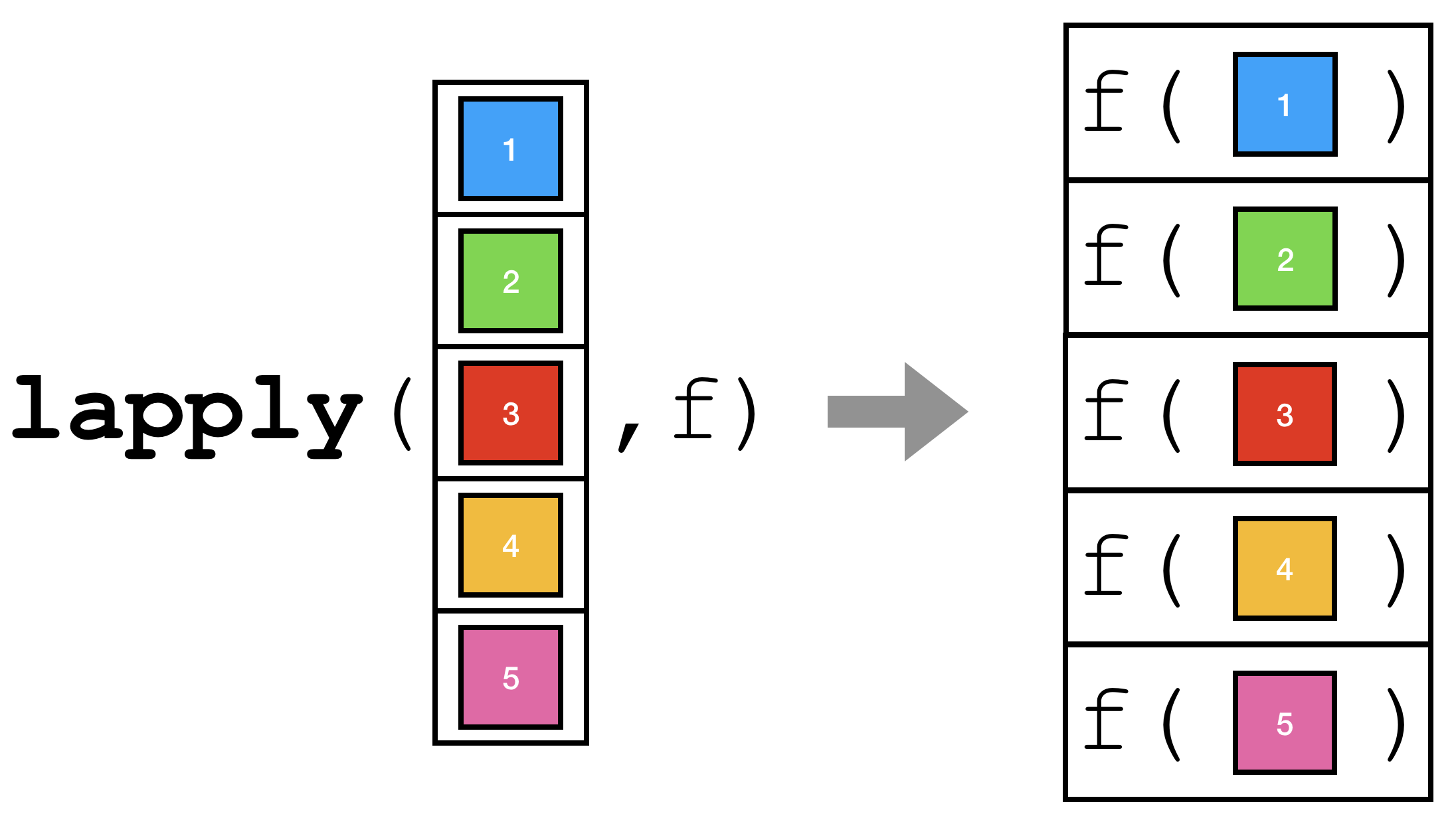
There are many functions, built-in and otherwise, to accomplish this task. We will begin by looking at the most important and generic function, lapply.

10.1.1 `lapply`

The function in R that performs the operation described above is the lapply function. The general syntax is:

lapply(X = some_list, FUN = f)

That is, some_list is a vector (atomic vector or list) that the function f will be “applied” to each element of. Note that it is customary to not name the arguments to lapply.

lapply(some_list, f)

Let’s start with a very simple example.

lapply(1:3, log)

#> [[1]]
#> [1] 0
#> 
#> [[2]]
#> [1] 0.6931472
#> 
#> [[3]]
#> [1] 1.098612

Here we see the log function applied to each of the elements of the vector 1:3. This would be the same as running the following:

list(
  log(1),
  log(2),
  log(3)
)

#> [[1]]
#> [1] 0
#> 
#> [[2]]
#> [1] 0.6931472
#> 
#> [[3]]
#> [1] 1.098612

Clearly, this isn’t a particularly useful example, as we could simply do the following:¹

log(1:3)

#> [1] 0.0000000 0.6931472 1.0986123

Although, note that lapply is returning a list, but the above returns an atomic vector. More on that in a moment.

For now, know that lapply will return a list that has the same length as the input vector.²

Let’s look at an example of iterating over a list.

set.seed(42)
ex_list = list(a = runif(5),
               b = runif(5),
               c = runif(5))

ex_list

#> $a
#> [1] 0.9148060 0.9370754 0.2861395 0.8304476 0.6417455
#> 
#> $b
#> [1] 0.5190959 0.7365883 0.1346666 0.6569923 0.7050648
#> 
#> $c
#> [1] 0.4577418 0.7191123 0.9346722 0.2554288 0.4622928

lapply(ex_list, max)

#> $a
#> [1] 0.9370754
#> 
#> $b
#> [1] 0.7365883
#> 
#> $c
#> [1] 0.9346722

Again, here the input was a list of length three, so the output is as well. You might wish the output was an atomic vector. Again, more on that soon.

lapply(ex_list, range)

#> $a
#> [1] 0.2861395 0.9370754
#> 
#> $b
#> [1] 0.1346666 0.7365883
#> 
#> $c
#> [1] 0.2554288 0.9346722

Finally, a slightly more useful example. This returns the same object as the following:

list(
  range(ex_list[[1]]),
  range(ex_list[[2]]),
  range(ex_list[[3]])
)

#> [[1]]
#> [1] 0.2861395 0.9370754
#> 
#> [[2]]
#> [1] 0.1346666 0.7365883
#> 
#> [[3]]
#> [1] 0.2554288 0.9346722

Hopefully, it is becoming clear that lapply can be used to write concise, useful, and readable code.

What if we want to use a function with more than one argument? For example:

multiply_and_power = function(x, c, p) {
  c * x ^ p
}

multiply_and_power(x = 2, c = 3, p = 0.5)

#> [1] 4.242641

multiply_and_power(x = 2, c = 1:3, p = 0.5)

#> [1] 1.414214 2.828427 4.242641

Be aware that depending on how we specify the values we pass to the arguments, there is likely going to be some length coercion taking place.

To use this function together with lapply, we simply add the values of the additional parameters as arguments to lapply.³

lapply(1:3, multiply_and_power, c = 1:5, p = 2)

#> [[1]]
#> [1] 1 2 3 4 5
#> 
#> [[2]]
#> [1]  4  8 12 16 20
#> 
#> [[3]]
#> [1]  9 18 27 36 45

What did this code do?

list(
  multiply_and_power(x = 1, c = 1:5, p = 2),
  multiply_and_power(x = 2, c = 1:5, p = 2),
  multiply_and_power(x = 3, c = 1:5, p = 2)
)

#> [[1]]
#> [1] 1 2 3 4 5
#> 
#> [[2]]
#> [1]  4  8 12 16 20
#> 
#> [[3]]
#> [1]  9 18 27 36 45

What if we wanted to iterate over a different argument, say c instead of x? Specify x and p in the call to lapply. Now lapply will iterate over c.

lapply(1:3, multiply_and_power, x = 1:5, p = 2)

#> [[1]]
#> [1]  1  4  9 16 25
#> 
#> [[2]]
#> [1]  2  8 18 32 50
#> 
#> [[3]]
#> [1]  3 12 27 48 75

So, this time, we did the following:

list(
  multiply_and_power(x = 1:5, c = 1, p = 2),
  multiply_and_power(x = 1:5, c = 2, p = 2),
  multiply_and_power(x = 1:5, c = 3, p = 2)
)

#> [[1]]
#> [1]  1  4  9 16 25
#> 
#> [[2]]
#> [1]  2  8 18 32 50
#> 
#> [[3]]
#> [1]  3 12 27 48 75

Sure, you could simply use this instead, but imagine needed to iterate over 1:100000 instead of 1:5.

10.1.2 `sapply`

Let’s return to the example that found the maximum of each element of a list.

set.seed(42)
ex_list = list(a = runif(5),
               b = runif(5),
               c = runif(5))

lapply(ex_list, max)

#> $a
#> [1] 0.9370754
#> 
#> $b
#> [1] 0.7365883
#> 
#> $c
#> [1] 0.9346722

As expected, the result is a list. However, notice that each element of said list is an atomic vector of length one, of the same type. We could actually check that using lapply.

lapply(lapply(ex_list, max), typeof)

#> $a
#> [1] "double"
#> 
#> $b
#> [1] "double"
#> 
#> $c
#> [1] "double"

lapply(lapply(ex_list, max), length)

#> $a
#> [1] 1
#> 
#> $b
#> [1] 1
#> 
#> $c
#> [1] 1

It probably seems like what we really want as output here is an atomic vector that is the same length as the input vector. We can obtain this result by switching from lapply to sapply.

sapply(ex_list, max)

#>         a         b         c 
#> 0.9370754 0.7365883 0.9346722

The s in sapply refers to the simplifying action taken by the function. Much of the details of how the simplification works follow the usual rules of the coercion hierarchy. It is probably best not to worry too much about these rules, but also not rely on simplification too much. Generally, it is best to use sapply in the case we’ve just seen here: you are certain the result of the function applied to each element is an atomic vector of length one, each with the same type.

Another example:

sapply(1:3, log)

#> [1] 0.0000000 0.6931472 1.0986123

But again, this example isn’t truly necessary, as the following is even better:

log(1:3)

#> [1] 0.0000000 0.6931472 1.0986123

We show this to demonstrate that many operations in R are already vectorized, so there is no need to iterate.

10.1.3 Other Apply Functions

Other apply functions exist. Many are rarely used. One that might be of interest is vapply which will do simplification like sapply, but the user will need to specify the expected outcome of each iteration, which will make the simplification more predictable.

vapply(1:3, log, double(1))

#> [1] 0.0000000 0.6931472 1.0986123

vapply(1:3, log, integer(1))

#> Error in vapply(1:3, log, integer(1)): values must be type 'integer',
#>  but FUN(X[[1]]) result is type 'double'

Another that you will likely see is the apply function. We would advise avoiding this unless you truly understand what it does. Also, beware, it should probably not be used with data frames.⁴

10.2 Loops

Loops are another form of control flow. They allow you to explicitly specify the repetition of some code, in contrast to the apply functions above that did so implicitly.⁵

Welcome to R Club.

The first rule of R Club is: Do not use for loops!

The second rule of R Club is: Do not use for loops!

And the third and final rule: If you have to use a for loop, do not grow vectors!

— Unknown

Loops are very common in programming, however, in R, it is probably best to avoid them unless you truly need them. The general heuristic you should use to determine if you need a loop or apply function is:

Use a loop when the result of the next iteration depends on the result of the previous iteration.
Use an apply function when the results of each iteration are independent.⁶

10.2.1 `for`

The most common looping structure is a for loop. The generic syntax is:

for (element in vector) {
  code_to_run
}

We’ll refer to element as the loop variable.

Let’s look at a specific example.

# pre-allocate storage vector
x = double(length = 5)

# perform loop
for (i in 1:5) {
  x[[i]] = i ^ 2
}

# check results
x

#> [1]  1  4  9 16 25

First, note that for is not a function, which is why you should consider placing a space between it and the parenthesis that follows. Next, (i in 1:5) is considered the header of the loop which defines how the iteration will take place. Here the name of the loop variable is i and it will take a value from the vector 1:5 each time the body runs. The code inside the braces, {} is called the body of the loop, much like the body of a function.

Each time through the loop, i, will take one of the values from 1:5. Or generally, the loop variable will take the value of each element of some vector.
For each value of i, the code x[i] = i ^ 2 will run. In general, for each value of the looping variable, the code in the body will run. And often, that code will depend on the looping variable, like we see here.

So, the above for loop ran each of the following:

x[[1]] = 1 ^ 2
x[[2]] = 2 ^ 2
x[[3]] = 3 ^ 2
x[[4]] = 4 ^ 2
x[[5]] = 5 ^ 2

This should make it clear that the purpose of a loop is to repeat code, without actually having to repeatedly type the code.

As has become a theme, this for loop is truly useless in R. We could have simply done:

(1:5) ^ 2

#> [1]  1  4  9 16 25

Here, i is functioning much like the name of a function argument, except now, we pass a new value, an element of 1:5, each time through the loop.

You can use any name you want for the loop variable, but i, j, and k are most common.

for (some_long_var_name in 1:5) {
  print(some_long_var_name)
}

#> [1] 1
#> [1] 2
#> [1] 3
#> [1] 4
#> [1] 5

A for loop is a very powerful structure, so it will not be possible for us to illustrate all possible usage examples. Let’s look at a correct loop written poorly, then the same loop written better, and try to draw some conclusion about best practices with for loops.

Before proceeding, let’s introduce the seq_along function.

seq_along(5:1)

#> [1] 1 2 3 4 5

Essentially, seq_along returns the indexes of a vector. Or, you could think of it as returning the result of the following:

1:length(5:1)

#> [1] 1 2 3 4 5

Let’s use a for loop to create a sequence of numbers. The first two numbers will be 10, and 5. Elements after that will be calculated as:

\[ x_i = 3 \cdot \frac{x_{i - 1}}{x_{i - 2}} \]

We’ll use a loop to create a sequence of length ten that follows this specification.

First, a bad example of how to write a loop to accomplish this:

# perform loop
for (i in 1:10) {
  if (i == 1) {
    x = 10
  } else if (i == 2) {
    x = c(x, 5)
  } else {
    x = c(x, 3 * x[i - 1] / x[i - 2])
  }
}

# check results
x

#>  [1] 10.0  5.0  1.5  0.9  1.8  6.0 10.0  5.0  1.5  0.9

We see the correct resulting vector, x, but we have used multiple sub-optimal techniques. In particular, we “grew” the x vector. The use of x = c(x, some_new_element) takes what was x, then creates a new x but combining the previous x with some new element. Do not do this. This is one of the reasons people incorrectly think R is slow. This operation is slow, but there is no need for it.

Instead, let’s pre-allocate the x which we will store our results in.

# pre-allocate x to be a double vector of the correct length
x = double(10) 

# perform loop
for (i in seq_along(x)) {
  if (i == 1) {
    x[[i]] = 10
  } else if (i == 2) {
    x[[i]] = 5
  } else {
    x[[i]] = 3 * x[i - 1] / x[i - 2]
  }
}

# check results
x

#>  [1] 10.0  5.0  1.5  0.9  1.8  6.0 10.0  5.0  1.5  0.9

This time, since x already existed, we are simply replacing individual elements of an already existing vector. This is faster. Any time you grow or add new elements (that is you increase the length of a vector) there is a copy operation taking place under the hood that you could have avoided.

Also, by pre-allocating x, we can now use seq_along(x). In some applications we might be creating x with a program, and we wouldn’t know its length ahead of time! This will avoid having to specify the length in two locations in code.

Some general ideas to keep in mind:

Do not attempt to iterate over and store results in the same vector.
Pre-allocate a “results” vector and update individual elements as you progress through the loop. Do not grow vectors.
Use seq_along and iterate over indexes rather than elements of a vector.

We’ve already discussed why the second item is a problem. Let’s now create an example that demonstrate items one and three.

The following function will check if an number is even.

is_even = function(x) {
  x %% 2 == 0
}

We also create a vector y that stores some numbers.

# create data
set.seed(42)
y = sample(1:10, size = 20, replace = TRUE)

# view data
y

#>  [1]  1  5  1  9 10  4  2 10  1  8  7  4  9  5  4 10  2  3  9  9

Our goal is to create a logical vector, the same length as y, containing TRUE at any index where y is even.

This will, not work:

for (i in y) {
  y[[i]] = is_even(i)
}

To better see the issue, temporarily place a print() statement inside the loop.⁷

# create data
set.seed(42)
y = sample(1:10, size = 20, replace = TRUE)

# perform loop
for (i in y) {
  print(i)
  y[[i]] = is_even(i)
}

#> [1] 1
#> [1] 5
#> [1] 1
#> [1] 9
#> [1] 10
#> [1] 4
#> [1] 2
#> [1] 10
#> [1] 1
#> [1] 8
#> [1] 7
#> [1] 4
#> [1] 9
#> [1] 5
#> [1] 4
#> [1] 10
#> [1] 2
#> [1] 3
#> [1] 9
#> [1] 9

# check results
y

#>  [1]  0  1  0  1  0  4  0  1  0  1  7  4  9  5  4 10  2  3  9  9

So i takes values from y, but by doing so, we don’t have access to the indexes at which we need to replace with the result of is_even. Let’s use seq_along.

# create data
set.seed(42)
y = sample(1:10, size = 20, replace = TRUE)

# perform loop
for (i in seq_along(y)) {
  y[[i]] = is_even(y[i])
}

# check results
y

#>  [1] 0 0 0 0 1 1 1 1 0 1 0 1 0 0 1 1 1 0 0 0

Note that inside of i, we now need to change i to y[i] to get the value rather than the index each time through the loop.

But there’s still an issue! We have 0 and 1 instead of FALSE and TRUE. Coercion!

# create data
set.seed(42)
y = sample(1:10, size = 20, replace = TRUE)

# pre-allocate storage vector
res = logical(length(y))

# perform loop
for (i in seq_along(y)) {
  res[[i]] = is_even(y[[i]])
}

# check results
res

#>  [1] FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE
#> [13] FALSE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE

Much better. But again, remember, many things in R are vectorized:

is_even(y)

#>  [1] FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE
#> [13] FALSE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE

This example did not need a loop, because results from one iteration to the next were independent. In the previous example, this was not the case, and was an example of when you truly need a loop.

Note that these examples have used atomic vectors, but, no reason we couldn’t use a list!

10.2.2 `while`

A while loop will repeat code until a specified condition is no longer met. The general syntax is:

while (condition) {
  code_to_run
}

Let’s see an example.

# create some data
x = 5

# pre-allocate storage vector
y = double(length = length(x))

# perform loop
while (x > 0) {
  print(x)
  y[[x]] = x ^ 2
  x = x - 1
}

#> [1] 5
#> [1] 4
#> [1] 3
#> [1] 2
#> [1] 1

# check results
x

#> [1] 0

#> [1]  1  4  9 16 25

Here, the loop runs until x is no longer greater than 0.

Notice that if we don’t modify x inside the loop, it would run forever! An infinite loop!⁸

You will likely see for loops more often, but while loops are useful when you don’t know how many iterations you’ll need ahead of time, but you can describe a stopping condition.

x = 1 # setup initial data
y = 0 # setup result vector

# perform loop
while(x > .Machine$double.eps) {
  y = y + x
  x = x / 2
}

# check results
y

This example demonstrates a method to numerically evaluate the following sum.⁹

\[ \sum_{k = 0}^{\infty} \left(\frac{1}{2}\right) ^ k \]

Because we cannot actually sum up an infinite number of terms, as that would take forever, we instead sum up all terms that are indistinguishable from zero to the computer. In this case, .Machine$double.eps gives us the smallest possible number that R can recognize on the machine that processed this chapter. Because x will only become smaller as the loop continues, we know that once the loop stops, all future terms would have also been indistinguishable from zero.

.Machine$double.eps

#> [1] 2.220446e-16

10.2.3 `repeat`

A repeat loop will continually repeat an expression, without ever stopping.

repeat {
  42
}

The above is not run, because it would never stop! It could have also been written using a while loop:

while (TRUE) {
  42
}

Because there is no built-in stopping rule when using repeat, it is not a feature we will return to often. If necessary, in order to exit a repeat loop, the break expression may be used.

x = 42
repeat {
  print(x)
  if (x < 1) {
    break
  }
  x = sqrt(x) - 1
}

#> [1] 42
#> [1] 5.480741
#> [1] 1.341098
#> [1] 0.1580579

10.3 Summary

TODO: You’ve learned to…

10.4 What’s Next?

TODO: ?

This example is easier to write, easier to read, and because of vectorization, much faster.↩︎
Think l for list. Although, it is unclear if that is the etymology of the name of the lapply function.↩︎
If you check the documentation for lapply, you’ll notice an argument called .... More on this later, but this is what allows R to pass these additional arguments to the function.↩︎
The apply function is useful when working with matrix objects, which so far we have been avoiding.↩︎
Technically, the apply functions could be said to be “hiding loops” as they are mostly just convenience functions wrapped around for loops.↩︎
Also check that you can’t just use a vectorized operation.↩︎
This is a simple and naive, but incredibly powerful debugging practice.↩︎
If you experience an infinite loop, use Ctrl + C in the console to escape it. Or press the stop button in RStudio.↩︎
Observant readers will recognize this sum as a geometric series and note that there is an analytical solution.↩︎

10.1 Apply Functions

10.1.1 lapply

10.1.2 sapply

10.1.3 Other Apply Functions

10.2 Loops

10.2.1 for

10.2.2 while

10.2.3 repeat